Primary SVM

SVM在1980年初由Vladimir Vapnik和Alexey Chervonenkis提出。

Motivation：对于一个线性二分类问题，假设一个点由$p$维向量表示，我们想要找到一个$p-1$维的hyperplane来区分这些点。以下的所有hyperplane都可以区分这两个类型，但是哪个hyperplane最佳？如何找到一个最佳的hyperplane？这是SVM最初需要解决的问题。

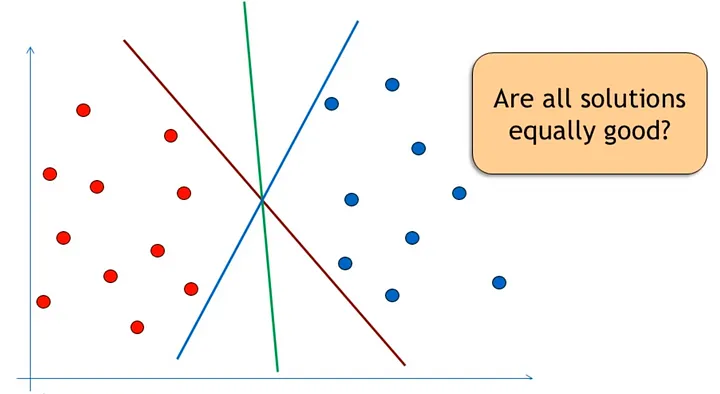
motivation

最佳hyperplane的一个合理选择是以最大间隔（margin）把两个类分开的超平面，这样可以防止模型的过拟合（generalization error）。

svm

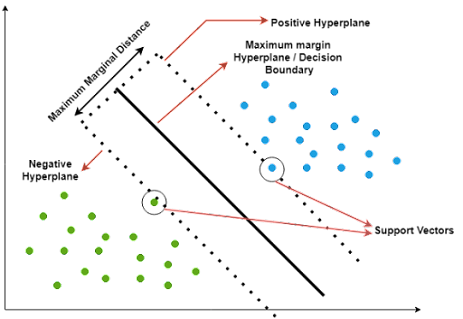
Terms：

Decision Boundary: 一个区分不同区域的的线/面。每一个区域都代表一个class，decision boundary可以用来预测新的数据属于哪一类。在SVM中，最优的decision boundary使得两个区域间的margin最大。
Hyperplan: 大于2维的decision boundery。
Support Vectors：用于计算最优decision boundary的数据点，也就是在negative/positive hyperplane上的点。
Margin Distance: 在训练集中离decision boundary最近的点的距离。
Kernal Function: 把数据映射到更高维空间的函数

Goal： maximization of margins between two different classes

Basic Math in Linear SVM

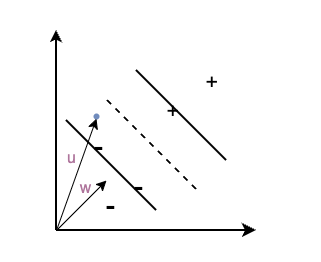
假设有这样一个二分类问题，如下图所示，“+”代表数据集里的正样本，“-”代表数据集里的负样本，虚线代表decision boundary，$\omega$ 是一个垂直于decision boundery的向量。对于一个新的数据（蓝色的原点），可以用向量$\mu$表示，我们如何确定它是正样本还是负样本？

可以知道，数据集里的所有负样本在$\omega$上的投影大小$<$所有正样本在$\omega$上的投影大小。所以对于一个新的样本，其在$\omega$上的投影大于某一个值c，我们就可以预测它为正样本，即 $\omega \cdot \mu \ge c$ ，也就是decision rule: $\omega \cdot \mu + b\ge 0,\ \ b=-c$ $SVM-math$
由于$\omega$仅仅垂直于decision boundary，其长度并不确定。求解出一个特定的$\omega$和$b$需要有更多的约束。因此，我们增加约束，其中$x_+$代表任意的正样本，$x_-$代表任意的负样本：

$\omega \cdot x_+ + b\ge 1$

$\omega \cdot x_- + b\le -1$
为了mathematical convenience，我们引入一个新的变量$y_i$

$y_i = +1\ \ for + samples$

$y_i = -1\ \ for - samples$
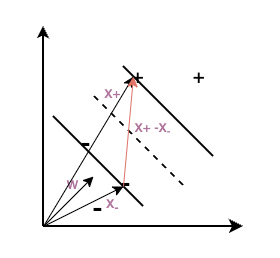
由此结合2和3两部，我们得到了一个适用于所有样本的式子，即 $y_i(\omega \cdot x_i + b)\ge 1\Rightarrow y_i(\omega \cdot x_i + b)-1 \ge 0$ 对于在gutter（negative/positive hyperplane）上的点， $y_i(\omega \cdot x_i + b)-1 = 0$ $SVM-math$
SVM的最终目标是要得到最大的margin，该长度可以表示为 $width=\frac{(x_+-x_-)\cdot \omega}{\Vert \omega\Vert}$ 由4可知，$x_+\cdot\omega=1-b,\ \ x_-\cdot\omega=-1-b$ 因此，$width=\frac{2}{\Vert \omega\Vert}$
我们需要得到最大的width，也就是最小的$\Vert \omega\Vert$, 即最小的$\frac{1}{2}\Vert \omega\Vert^2$ （仅仅是为了数学运算的方便，凑出来的，又称regularizer）
在约束条件下，求解最值问题需要用到拉格朗日乘数法。在现在的情况下，约束条件为：$y_i(\omega \cdot x_i + b)-1 \ge 0$ 求解的最值为：找到$\omega$ ，$b$使得$min\ \frac{1}{2}\Vert \omega\Vert^2$ $\omega$ ，$b$， $\alpha_i$为未知数，其他值均已知 $L(\omega, b, \alpha) = \frac{1}{2}\Vert \omega\Vert^2 - \sum \alpha_i[y_i(\omega \cdot x_i + b)-1]$
目前要求解$L$的极值

$\frac{dL}{d\omega}=\omega-\sum\alpha_iy_ix_i=0$

$\frac{dL}{db}=-\sum\alpha_iy_i=0$
回代$\omega$ 和$b$到$L$ $L=\sum \alpha_i-\frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_jx_ix_j$ 此时，$L$的极值仅仅和$x_i\cdot x_j$有关 Decision rule现在变成，也仅仅和$x_i\cdot \mu$有关 $\sum\alpha_iy_ix_i\cdot\mu+b\ge0$
总结一下，对SVM的建模：
- primal problem:
  
  $MIN_{\omega,b} \frac{1}{2}\Vert \omega\Vert^2 \ \ s.t.\ \ y_i(\omega \cdot x_i + b)-1 \ge 0$
- dual problem ($L$的极值问题):
  
  $L=\sum \alpha_i-\frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_jx_ix_j,\ \ \alpha_i \ge0$

使用数学分析中的方法，如gradient desecnt optimization来求解上述的数学问题，得到最优的$\omega$和$b$。

Soft Margin SVM

Motivation: 对于如下问题，SVM不能够找到一个最优的hyperplane来区分两种样本，因此需要引入soft margin，来允许一些错误的发生。当预测错误时，需要得到一些penalty/errors。

soft

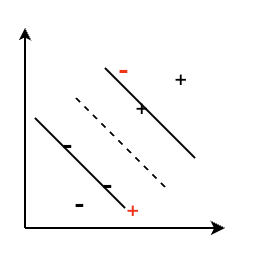
因此，soft margin SVM的问题可以被定义为：

Primal problem

$min\ \frac{1}{2}\Vert \omega\Vert^2 + \underbrace{C_i\sum_{i=1}^n \zeta_i}_{error\ term}$
dual promblem:

$L=\sum \alpha_i-\frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_jx_ix_j,\ \ 0\le \alpha_i \le C$

这个error term可以防止模型的过拟合。

那么该如何定义这个error呢？在预测正确时，penalty应该为0；在预测错了，但是错得不离谱时penalty会比较小；当预测错得很离谱时，penalty应该很大。有一个Loss function符合上述特点，即Hinge Loss，$y_i$表示真实值，$(\omega \cdot x_i + b)$表示预测值:

$max(0, 1-y_i(\omega \cdot x_i + b))$

因此，soft margin SVM的问题可以被定义为：

$MIN_{\omega,b} (C_i\sum max[0, 1-y_i(\omega \cdot x_i + b)] \ +\frac{1}{2} \Vert \omega\Vert^2)$

Non-linear SVM

Motivation: 对于如下问题，SVM不能够找到一个最优的hyperplane来区分两种样本，但是在更高维度上，这两类样本是可以被区分的，因此需要引入kernel function $\Phi$，来把数据映射到更高的纬度上，从而使用SVM来对模型进行分类。

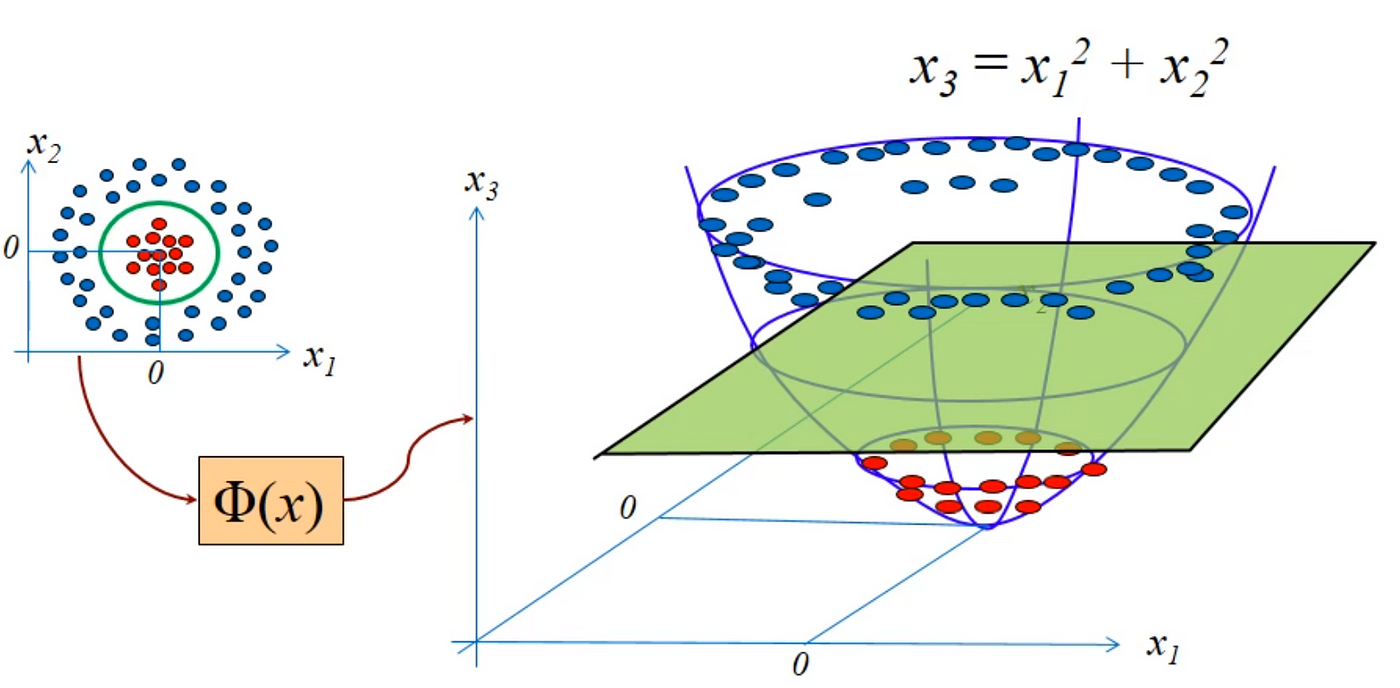
non-linear

常用的kernel function有：

To be continued…

手撕SVM

To be continued…

Support Vector Machine (SVM) Learning notes

Primary SVM

Basic Math in Linear SVM

Soft Margin SVM

Non-linear SVM

手撕SVM

Reference

Enjoy Reading This Article?